How I over-engineered a Fast Fourier Transform for Arduino.
The lengthy, excruciating, details.
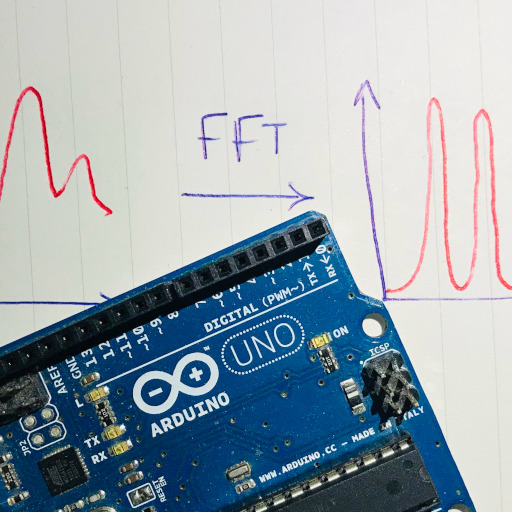
Everything began with me wanting to implement the Fast Fourier Transform (FFT) on my Arduino Uno for a side project. The first thing you do in such case is asked your favorite search engine for existing solutions. If you google "arduino FFT" one of the first result will be related to this instructable: ApproxFFT: The Fastest FFT Function for Arduino. As you can imagine, this could only tickle my interest: there was an existing solution to my problem, and the title suggested that it was the fastest available! And thus, on April 18ᵗʰ 2021, I started a journey that would bring me to write my own tutorial on implementing the FFT in Julia, learn AVR Assembly and write a blog post about it, about one year and a half later.
A nice approximation of the norm of a 2D vector.
Some cool sunday project!
While wandering on the internet, I stumbled uppon Paul Hsieh's blog-post, where he demonstrates a way to approximate the norm of a vector without any call to the sqrt function. Let's see if I can reproduce the steps to derive this.
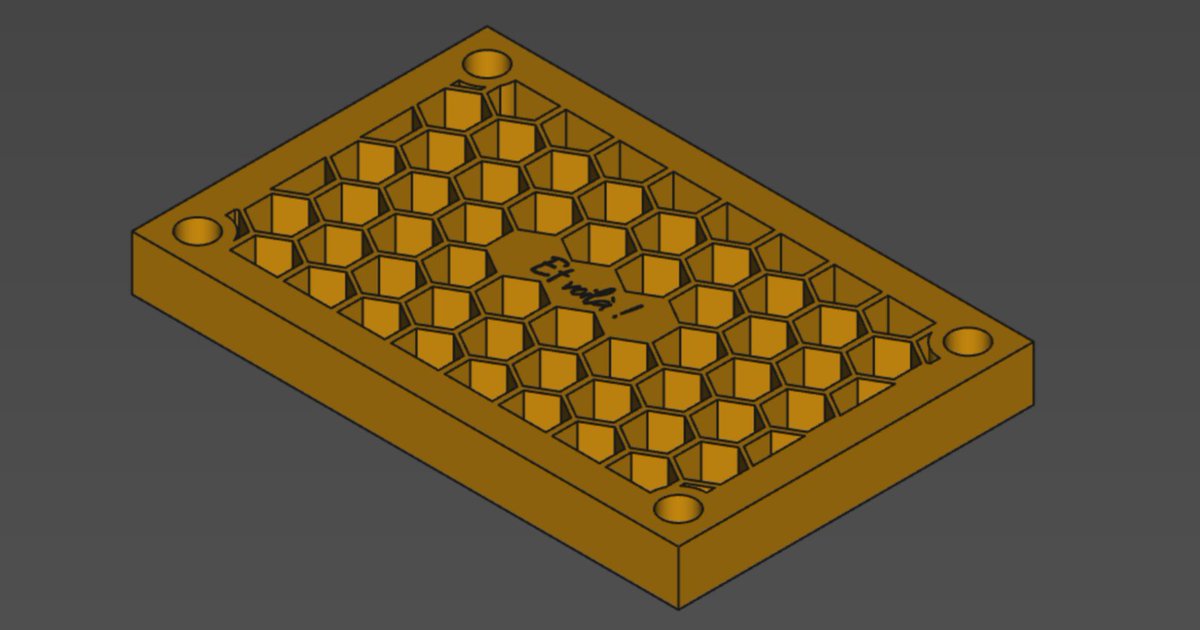
Modeling a honeycomb grid in FreeCAD
A small tutorial on FreeCAD
Someone asked me how to make a honeycomb grid in @FreeCADNews. Here's how I do it, and bonus it's parametric! ⬇️
Let's play at implementing a fast Fourier transform!
An algorithm you probably use on a daily basis.
The Fourier transform is an essential tool in many fields, be it in Physics, Signal Processing, or Mathematics. The method that is probably the most known to calculate it numerically is called the FFT for Fast Fourier Transform. In this little tutorial, I propose to try to understand and implement this algorithm in an efficient way. I will use the language Julia, but it should be possible to follow using other languages such as Python or C. We will compare the results obtained with those given by the Julia port of the FFTW library.